Um robot que desenha

Etiquetas: Arduino, Braço robótico, C/C++, Cinemática inversa, Programação

O projeto aqui apresentado consiste em desenhar um braço robótico com um lápis numa folha de papel. Um ótimo exercício de programação e controlo de um braço robótico.

Hardware

• Braço robótico prático
• 4x Servomotor SMS1012
• Controlador de servomotor ou shield de servo
• Fonte de alimentação de 5V
• Cabo USB
• Placa Arduino UNO

Objetivo

Objetivo: Desenhar um círculo utilizando um braço robótico

Para levar a cabo este projeto, precisamos de

• Montagem do braço robótico (Estrutura)
• Realizar a montagem eletrónica para controlar o braço e a alimentação eléctrica (Hardware)
• Desenvolver o programa para controlar a sequência de servomotores de modo a descrever uma forma no espaço (Software)

Braço robótico

Objeto: A estrutura deve ser capaz de transportar um lápis e de se deslocar nas três dimensões do espaço.

O braço Handy está a ser utilizado para este projeto. Os motores escolhidos são micro-servomotores 9g leves, económicos e fáceis de utilizar.

O braço é montado com os seus servomotores e o seu suporte é fixado a uma placa. Para este projeto também desenhámos e imprimimos um suporte para lápis, que pode descarregar aqui.

Hardware

Objetivo: A eletrónica deve ser capaz de distribuir a alimentação de energia à placa de comando e aos servomotores e de acionar os servomotores através de um sinal PWM.

• Arduino UNO

As placas Arduino são fáceis de utilizar, com um grande número de bibliotecas disponíveis e uma enorme comunidade de apoio. Como o programa requer um pouco de RAM, optámos pela placa Arduino UNO.

A placa arduino é alimentada pelo PC ou pelo cabo USB.

• Acionamento do servomotor

A placa Arduino não consegue alimentar tantos servomotores, pelo que é necessário adicionar um controlador ao conjunto.

Um driver de servomotor foi construído seguindo este tutorial, e é alimentado por baterias em série.

Software

Objetivo du programme

Vamos escrever os objectivos do programa e dividi-los em tarefas a realizar

• Descrever as coordenadas da forma no espaço
• Transformar as coordenadas espaciais do círculo nos ângulos das articulações do robot.
• Verificação da posição do robot
• Converter os ângulos do robô em comandos do servomotor
• Envio de um comando para o atuador

Descrever as coordenadas da forma no espaço

A forma escolhida é uma circunferência pela sua simplicidade. As equações paramétricas de uma circunferência no espaço são:

Para a coordenada z, consideramos o tamanho do lápis, ou seja, 20 mm.

Escrevemos uma função que devolve a posição alvo do robot Xd como uma função do passo de tempo:

void circleTraj(double R,double x,double y,double z,int i,double Te, float Xd[6]){
        Xd[0]=x+R*cos(2*PI*Te*i);
        Xd[1]=y+R*sin(2*PI*Te*i);
        Xd[2]=z;
        Xd[3]=0;
        Xd[4]=0;
        Xd[5]=0;
}

Transformar as coordenadas espaciais do círculo nos ângulos das articulações do robot.

O braço robótico pode ser descrito como uma cadeia robótica utilizando o método Denavit-Hartenberg. Este método é útil para controlar um braço com mais de três articulações.

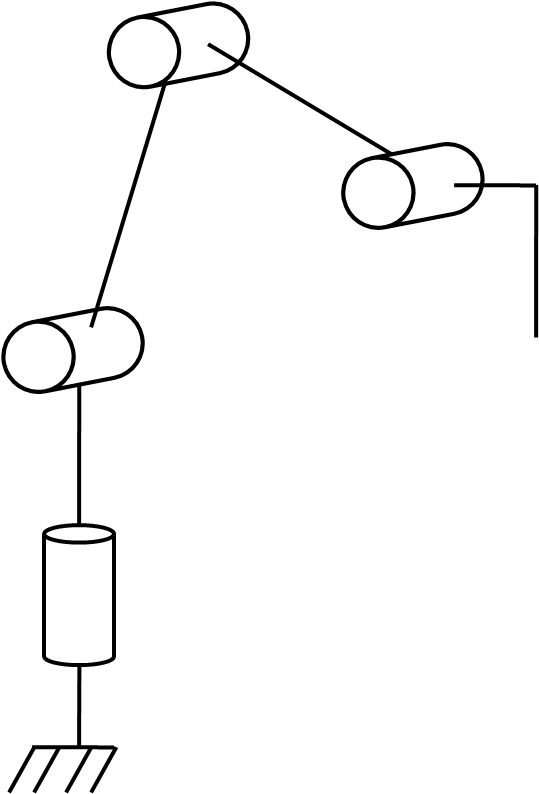
Este método consiste em definir um sistema de coordenadas cartesianas para cada articulação, seguindo a mesma lógica, o que permite definir parâmetros para descrever matematicamente os movimentos de cada elo no espaço.

Definir os parâmetros para cada ligação robótica com base na geometria (parâmetro DH)

j	Sigmaj	Thetaj	Dj (mm)	Aj (mm)	alphaj
1	0	Th1	45	0	90
2	0	Th2	0	75	0
3	0	Th3	0	75	0
4	0	Th4	4	0	-90

O cálculo dos ângulos desejados do motor em função da posição desejada envolve a inversão da matriz Jacobiana definida com os parâmetros DH. Para os cálculos da matriz, utilizamos a biblioteca MatrixMath.h‘.

void computeAngle(){
    float J[6][nbLinks];
    float Jt[nbLinks][6];
    float JJt[nbLinks][nbLinks];
    float invJ[nbLinks][6];
    double detJ;
        //    compute jacobian
        jacobian(sig,a,al,d,th,q,nbLinks,(float*)J);

        // avoid singularity
        Matrix.Transpose((float*)J,6,nbLinks,(float*)Jt);
        Matrix.Multiply((float*)Jt, (float*)J, nbLinks, 6, nbLinks,(float*)JJt);

        
        detJ=detrm(JJt,nbLinks);
        // invert jacobian
        if(detJ>=1){
          Matrix.Invert((float*)JJt,nbLinks);
          Matrix.Multiply((float*)JJt,(float*)Jt,nbLinks,nbLinks,6,(float*)invJ);
        }
        
        for(int i=0;i<nbLinks;i++){
                qu[i]=0;
            for(int j=0;j<6;j++){
                qu[i]+=invJ[i][j]*Xu[j];
            }
        }
}

Função para converter os ângulos do robô em comandos para o servomotor

A conversão dos ângulos em controlo PWM depende do posicionamento dos servomotores, dos valores nominais de PWM e da convenção dos pontos de referência cartesianos utilizados para descrever as articulações do robô no espaço.

Servo/Joint	Min impulse	Max impulse	Min robot	Max robot
1	500	2500	-PI/2	PI/2
2	500	2500	PI	0
3	600	2600	-PI/2	PI/2
4	500	2500	-PI/2	PI/2

int jointToImp(double x,int i) {
        int imp=(x - joint_min[i]) * (imp_max[i]-imp_min[i]) / (joint_max[i]-joint_min[i]) + imp_min[i];
        imp=max(imp,imp_min[i]);
        imp=min(imp,imp_max[i]);
        return imp;  
}

Envio de um comando para o atuador

Para controlar os servomotores, usamos a biblioteca Servo.h disponível como padrão no IDE do Arduino. Escrevemos uma função que envia o comando PWM para cada servomotor de acordo com o ângulo solicitado.

void servoToImp(double q[nbLinks],int velocity){
  for (int i=0; i<nbLinks; i++) {
    servo[i].writeMicroseconds(jointToImp(q[i],i));
    delay(velocity);  
    }
}

Função de controlo do robô

Para controlar os servomotores, a posição desejada do robô deve ser sempre comparada com a sua posição atual.

Assim, calculamos a posição do robot em função dos ângulos do motor. Para o efeito, utilizamos as matrizes de transformação definidas pelo método de Denavit-Hartenberg.

        forwardKinematics(sig,a,al,d,th,q,nbLinks,X);

Aplicar o controlador para calcular a posição seguinte do robot

        circleTraj(20,165,0,20,k,Te,Xd);
        circleTraj(20,165,0,20,k+1,Te,Xk);
        for(int i=0;i<6;i++) Xu[i]=(Xk[i]-Xd[i]+gain*Te*(Xd[i]-X[i]));

Determinamos os ângulos do motor para atingir a posição seguinte

        for(int i=0;i<nbLinks;i++) qN1[i]=q[i];
        computeAngle();
        for(int i=0;i<nbLinks;i++) q[i]=qN1[i]+qu[i];

O controlo PWM é aplicado a cada servomotor

        servoToImp(q,10);

Código completo

Biblioteca personalizada de MatrixMath.h, MatrixMathExt.h

/*****************************************************************\
* Project : Handy
* Author : X. Wiedmer 
* Version : V01
* Date : 08/06/2017
* Revision : 
* Summary :
\*****************************************************************/
// Library
#include <SoftwareSerial.h>
#include <Servo.h>
#include <MatrixMathExt.h>

// Pin assignement
#define BASE 2 
#define SHOULDER 3 
#define ARM 4 
#define FOREARM 5
#define WRIST 6

//paramètres Denavit-Hartenberg
    const double baseLength = 45;//mm
    const double shoulderLength = 10;//mm
    const double armLength = 75;//mm
    const double forearmLength = 75;//mm
    const double wristLength = 40;//mm

    const int nbLinks=4;
    double sig[nbLinks]={0,0,0,0};
    double a[nbLinks]={0,armLength,forearmLength,wristLength};
    double al[nbLinks]={PI/2,0,0,0};
    double d[nbLinks]={baseLength,0,0,0};
    double th[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2};
    
    double restPos[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2};
    
    
//paramètres servomoteur
    const int servoPin[nbLinks]={BASE,SHOULDER,ARM,FOREARM};
    Servo servo[nbLinks];
    const double joint_min[nbLinks]={-PI/2,PI,-2*PI/3,-PI/2};
    const double joint_max[nbLinks]={PI/2,0,PI/2,PI/2};
    const int imp_min[nbLinks]={500,500,600,500};
    const int imp_max[nbLinks]={2500,2500,2600,2500};

//paramètre du contrôle
    double Te=0.01; // pas de temps du contrôleur
    double gain=30; // gain du contrôle
    int N=(int)2/Te+1; // nombre d'étape pour parcourir 2 fois le cercle

// Variables
    float X[6],Xd[6],Xk[6],Xu[6];
    double qN1[nbLinks],qu[nbLinks];
    double q[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2};

    int firstShot = 0; // Pour que le programme ne s'exécute qu'une fois


/******************************************************************\
* PRIVATE FUNCTION: setup
*
* PARAMETERS:
* ~ void
*
* RETURN:
* ~ void
*
* DESCRIPTIONS:
* Initiate inputs/outputs
*
\******************************************************************/
void setup(){
  Serial.begin(9600); // Initialise le port série

  for (int i=0; i<nbLinks; i++) { // Initiatlise et positionne les servomoteurs au démarrage
    servo[i].writeMicroseconds(jointToImp(0,i));
    servo[i].attach(servoPin[i]);
    delay(500);
  }
}

/******************************************************************\
* PRIVATE FUNCTION: loop
*
* PARAMETERS:
* ~ void
*
* RETURN:
* ~ void
*
* DESCRIPTIONS:
* Main Function of the code 
\******************************************************************/
void loop(){
  if (firstShot == 0){
    //follow trajectory
    for(int k=0;k<N;k++){

        //Calcule la position du robot
        forwardKinematics(sig,a,al,d,th,q,nbLinks,X);

        //Calcule la prochaine position
        circleTraj(20,165,0,20,k,Te,Xd);
        circleTraj(20,165,0,20,k+1,Te,Xk);
        for(int i=0;i<6;i++) Xu[i]=(Xk[i]-Xd[i]+gain*Te*(Xd[i]-X[i]));
        
        //Calcule les angles moteurs pour atteindre la prochaine position
        for(int i=0;i<nbLinks;i++) qN1[i]=q[i];
        computeAngle();
        for(int i=0;i<nbLinks;i++) q[i]=qN1[i]+qu[i];
        
        //Envoie la commande au servomoteur
        servoToImp(q,10);

        // Affiche les angles moteur à chaque itération
        Serial.print("-----------------Iteration ");
        Serial.println(k);
        Serial.print("angle base = ");
        Serial.println(q[0]);
        Serial.print("angle bras = ");
        Serial.println(q[1]);
        Serial.print("angle avant-bras = ");
        Serial.println(q[2]);
        Serial.print("angle poignet = ");
        Serial.println(q[3]);
    }
    firstShot=1;
  }
  if(firstShot==1){
    Serial.println("robot au repos");
    restR();
    Serial.println("robot stop");
    stopR();
    firstShot=2;
  }
  
  }

// Decrit la trajectoire dans l'espace en focntion du temps
void circleTraj(double R,double x,double y,double z,int i,double Te, float Xd[6]){
        Xd[0]=x+R*cos(2*PI*Te*i);
        Xd[1]=y+R*sin(2*PI*Te*i);
        Xd[2]=z;
        Xd[3]=0;
        Xd[4]=0;
        Xd[5]=0;
}

// Calcule la matrice de transformation d'un lien robotique
void computeLinkTransform(double a,double al,double d, double th, float T[][4]){
    float trans[4][4] = {{cos(th),  -sin(th)*cos(al),  sin(th)*sin(al), a*cos(th)},
          {sin(th),   cos(th)*cos(al), -cos(th)*sin(al), a*sin(th)},
          {     0,            sin(al),         cos(al),        d      },
          {     0,                 0,               0,            1      } };
    Matrix.Copy((float*)trans,4,4,(float*)T);
}

// Calcule la position de la chaine robotique
void forwardKinematics(double* sig,double* a,double* al,double* d,double* th,double* q, int nbLinks, float X[6]){
    float A[4][4]={{1, 0, 0, 0},
           {0, 1, 0, 0},
           {0, 0, 1, 0},
           {0, 0, 0, 1}};
    float R[4][4];
    float Ti[4][4];

    // Compute transformation matrix
    for (int i=0; i<nbLinks; i++){
        if (sig[i]==0){
            th[i]=q[i];
        }else{
            d[i]=q[i];
        }
        //A=A*Ti
        computeLinkTransform(a[i],al[i],d[i],th[i],Ti);
        Matrix.Multiply((float*)A, (float*)Ti,4, 4,4, (float*)R);
        Matrix.Copy((float*)R,4,4,(float*)A);
    }

    X[0]=A[0][3];
    X[1]=A[1][3];
    X[2]=A[2][3];
    X[3]=0;
    X[4]=0;
    X[5]=0;
}

// Calcule un produit vectoriel
void CrossProduct1D(float* a, float* b, float* r){
    /*Ex: double v1[3]={1,0,0};
    double v2[3]={0,0,1};
    double w[3];
    CrossProduct1D(v1,v2,w);*/

  r[0] = a[1]*b[2]-a[2]*b[1];
  r[1] = a[2]*b[0]-a[0]*b[2];
  r[2] = a[0]*b[1]-a[1]*b[0];

}

// Calcule la matrice jacobienne d'une chaine robotique
void jacobian(double* sig,double* a,double* al,double* d,double* th,double* q, int nbLinks, float* J){
    float Ti[4][4];
    float O[nbLinks+1][3];
    float z[nbLinks+1][3];
    float A[4][4]={{1, 0, 0, 0},
       {0, 1, 0, 0},
       {0, 0, 1, 0},
       {0, 0, 0, 1}};
    float R[4][4];
    float v[4];
    O[0][0]=0;
    O[0][1]=0;
    O[0][2]=0;
    
    z[0][0]=0;
    z[0][1]=0;
    z[0][2]=1;
    
    float v0[4]={0,0,1,1};
    
    for (int i=0; i<nbLinks; i++){
    
        // Compute transformation matrix
        if (sig[i]==0){
            th[i]=q[i];
        }else{
            d[i]=q[i];
        }
        computeLinkTransform(a[i],al[i],d[i],th[i],Ti);
        // A=A*T[j];
        Matrix.Multiply((float*)A, (float*)Ti,4, 4,4, (float*)R);
        Matrix.Copy((float*)R,4,4,(float*)A);
        //Compute joint center and orientation vector
        O[i+1][0]=A[0][3];
        O[i+1][1]=A[1][3];
        O[i+1][2]=A[2][3];
    
        Matrix.Multiply((float*)A, (float*)v0,4, 4,1, (float*)v);
        //z{i}=[v(1); v(2); v(3)]-O{i};
        z[i+1][0]=v[0]-O[i+1][0];
        z[i+1][1]=v[1]-O[i+1][1];
        z[i+1][2]=v[2]-O[i+1][2];
    
    }
    
    //Jacobian
    float tempv[3];
    float cprod[3];
    
    for(int i=0;i<nbLinks;i++){
        if (sig[i]==0){
            // Ji=[z(i-1)xON-O(i-1); z(i-1)]
            Matrix.Subtract((float*)O[nbLinks], (float*)O[i],1,3,(float*)tempv);
            CrossProduct1D(z[i],tempv,cprod);
            J[0*nbLinks+i]=cprod[0];
            J[1*nbLinks+i]=cprod[1];
            J[2*nbLinks+i]=cprod[2];
            J[3*nbLinks+i]=z[i][0];
            J[4*nbLinks+i]=z[i][1];
            J[5*nbLinks+i]=z[i][2];
        }else{
            J[0*nbLinks+i]=z[i][0];
            J[1*nbLinks+i]=z[i][1];
            J[2*nbLinks+i]=z[i][2];
            J[3*nbLinks+i]=0;
            J[4*nbLinks+i]=0;
            J[5*nbLinks+i]=0;
        }
    }
}

// Calcul le déterminant d'une matrice
float detrm(float a[nbLinks][nbLinks],float k)
{
  float s=1,det=0,b[nbLinks][nbLinks];
  int i,j,m,n,c;
  if(k==1)
  {
    return(a[0][0]);
  }
  else
  {
    det=0;
    for(c=0;c<k;c++)
    {
      m=0;
      n=0;
      for(i=0;i<k;i++)
      {
        for(j=0;j<k;j++)
        {
          b[i][j]=0;
          if(i!=0&&j!=c)
          {
            b[m][n]=a[i][j];
            if(n<(k-2))
              n++;
            else
            {
              n=0;
              m++;
            }
          }
        }
      }
      det=det+s*(a[0][c]*detrm(b,k-1));
      s=-1*s;
      }
  }
  return(det);
}
// Calcule les angles moteur en fonction de la position désirée
void computeAngle(){
    float J[6][nbLinks];
    float Jt[nbLinks][6];
    float JJt[nbLinks][nbLinks];
    float invJ[nbLinks][6];
    double detJ;
        //    compute jacobian
        jacobian(sig,a,al,d,th,q,nbLinks,(float*)J);

        // avoid singularity
        Matrix.Transpose((float*)J,6,nbLinks,(float*)Jt);
        Matrix.Multiply((float*)Jt, (float*)J, nbLinks, 6, nbLinks,(float*)JJt);

        
        detJ=detrm(JJt,nbLinks);
        // invert jacobian
        if(detJ>=1){
          Matrix.Invert((float*)JJt,nbLinks);
          Matrix.Multiply((float*)JJt,(float*)Jt,nbLinks,nbLinks,6,(float*)invJ);
        }
        
        for(int i=0;i<nbLinks;i++){
                qu[i]=0;
            for(int j=0;j<6;j++){
                qu[i]+=invJ[i][j]*Xu[j];
            }
        }
}

// Convertie l'angle moteur en commande PWM
int jointToImp(double x,int i) {
        int imp=(x - joint_min[i]) * (imp_max[i]-imp_min[i]) / (joint_max[i]-joint_min[i]) + imp_min[i];
        imp=max(imp,imp_min[i]);
        imp=min(imp,imp_max[i]);
        return imp;  
}

// Intitialise servomoteur
void servoAttach(){
  for (int i=0; i<nbLinks; i++) {
    servo[i].attach(servoPin[i]);
  }   
}

// Envoie la commande PWM à chaque servomoteur
void servoToImp(double q[nbLinks],int velocity){
  for (int i=0; i<nbLinks; i++) {
    servo[i].writeMicroseconds(jointToImp(q[i],i));
    delay(velocity);  
    }
}

// Met le robot en position de repos
void restR(){
  servoToImp(restPos,500);
}

// Déconnecte les servomoteurs
void stopR(){
  for(int j=0;j<nbLinks;j++){
    servo[j].detach();
  }
}

Resultados

O motor desenha na folha e segue a trajetória definida.

Se quiser ajuda com o seu braço robótico ou quiser mais informações sobre este projeto, deixe um comentário ou contacte-nos.

Referência

• programação com Arduino
• Controlar um servomotor com o Arduino
• Método Denavit-Hartenberg (vídeo)