Le projet présenté ici consiste à faire dessiner un bras robotisé muni d’un crayon sur une feuille de papier. Un très bon exercice pour programmer et piloter correctement un bras robotisé.
Matériel
- Bras robotisé Handy
- 4x Servomoteur SMS1012
- Driver de servomoteurs ou servo shield
- alimentation 5V
- Câble USB
- Carte Arduino UNO
Objectif
Obj: Dessiner un cercle à l’aide d’un bras robotisé
Pour réaliser ce projet il nous faut:
- Monter le bras robotisé (Structure)
- Réaliser le montage électronique permettant le contrôle du bras et l’alimentation électrique (Hardware)
- Développer le programme permettant de piloter la séquence de servomoteur afin de décrire une forme dans l’espace (Software)
Bras robotisé
Obj: La structure doit pouvoir porter un crayon et se déplacer dans les trois dimensions de l’espace.
Le bras Handy est utilisé pour ce projet. Les moteurs choisis sont des micro servomoteur 9g léger, bon marché et simple d’utilisation.
Le bras est monté avec ses servomoteurs et son support est fixé à une planche. Pour ce projet nous avons aussi dessiné et imprimé un porte crayon que vous pouvez télécharger ici.

Hardware
Obj: L’électronique doit pourvoir distribuer l’alimentation à la carte de contrôle ainsi qu’aux servomoteurs et piloter les servomoteurs à l’aide d’un signal PWM.
- Arduino UNO
Les cartes Arduino sont simple d’utilisation, de nombreuses librairies sont disponibles et disposent d’une communauté d’entraide importante. Le programme nécessitant un peu de mémoire vive, nous avons opté pou la carte Arduino UNO.
La carte arduino est alimentée soit le PC à l’aide du câble USB.
- Driver de servomoteur
La carte Arduino ne peut pas alimenter autant de servomoteurs il est donc nécessaire d’ajouter un driver au montage.
Un driver de servomoteurs a été fabriqué en suivant ce tutoriel, et est alimenté à l’aide de piles en série.

Software
Objectif du programme
Couchons sur papier les objectifs du programme et déclinons-les en tâches à réaliser
- Décrire les coordonnées de la forme dans l’espace
- Transformer les coordonnées dans l’espace du cercle en angle des articulations du robot.
- Contrôler la position du robot
- Convertir les angles du robot en en commande pour le servomoteur
- Envoyer une commande au servomoteur
Décrire les coordonnées de la forme dans l’espace
La forme choisie est un cercle pour sa simplicité. Les équations paramétriques d’un cercle dans l’espace sont:
Pour la coordonnée en z nous prenons la taille du crayon soit 20mm.
Nous écrivons une fonction qui retourne la position cible Xd du robot en fonction du pas de temps:
void circleTraj(double R,double x,double y,double z,int i,double Te, float Xd[6]){ Xd[0]=x+R*cos(2*PI*Te*i); Xd[1]=y+R*sin(2*PI*Te*i); Xd[2]=z; Xd[3]=0; Xd[4]=0; Xd[5]=0; }
Transformer les coordonnées dans l’espace du cercle en angle des articulations du robot.
Le bras robotisé peut être décrit comme une chaine robotique par la méthode de Denavit-Hartenberg. Cette méthode est intéressante pour piloter un bras avec plus de trois articulations.
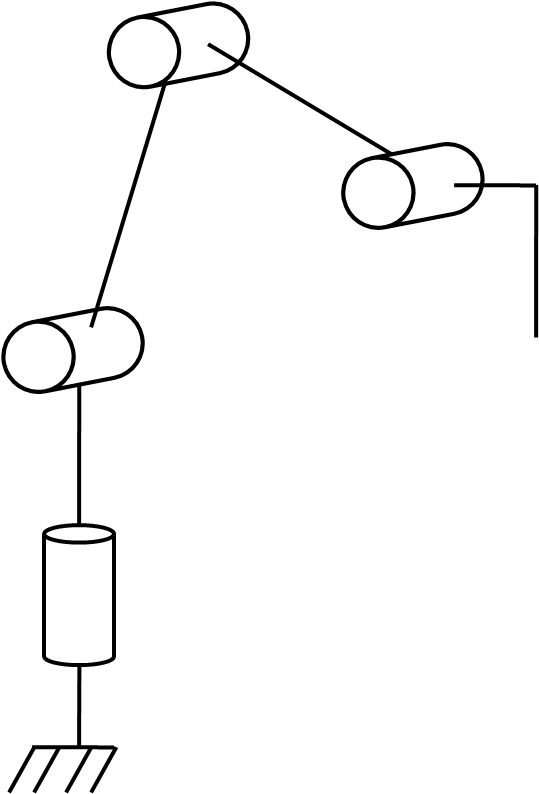
Cette méthode consiste à définir un repère cartésien pour chaque articulation en suivant la même logique et qui permet de définir des paramètres pour décrire mathématiquement les mouvements de chaque lien dans l’espace.
Définir les paramètres de chaque lien robotique en fonction de la géométrie(paramètre DH)
| j | Sigmaj | Thetaj | Dj (mm) | Aj (mm) | alphaj |
| 1 | 0 | Th1 | 45 | 0 | 90 |
| 2 | 0 | Th2 | 0 | 75 | 0 |
| 3 | 0 | Th3 | 0 | 75 | 0 |
| 4 | 0 | Th4 | 4 | 0 | -90 |
Le calcul des angles moteurs désirés en fonction de la position désirée passe par l’inversion de la matrice Jacobienne définie à l’aide des paramètres DH. Pour les calculs matriciels, nous utilisons la librairie MatrixMath.h
void computeAngle(){ float J[6][nbLinks]; float Jt[nbLinks][6]; float JJt[nbLinks][nbLinks]; float invJ[nbLinks][6]; double detJ; // compute jacobian jacobian(sig,a,al,d,th,q,nbLinks,(float*)J); // avoid singularity Matrix.Transpose((float*)J,6,nbLinks,(float*)Jt); Matrix.Multiply((float*)Jt, (float*)J, nbLinks, 6, nbLinks,(float*)JJt); detJ=detrm(JJt,nbLinks); // invert jacobian if(detJ>=1){ Matrix.Invert((float*)JJt,nbLinks); Matrix.Multiply((float*)JJt,(float*)Jt,nbLinks,nbLinks,6,(float*)invJ); } for(int i=0;i<nbLinks;i++){ qu[i]=0; for(int j=0;j<6;j++){ qu[i]+=invJ[i][j]*Xu[j]; } } }
Fonction permettant de convertir les angles du robot en commande pour le servomoteur
La conversion des angles en commande PWM dépend du positionnement des servomoteurs, des valeurs nominales de PWM, ainsi que de la convention des repères cartésiens utilisés pour décrire les articulations du robot dans l’espace.
La conversion est différente pour chaque servomoteur.
| Servo/Joint | Min impulse | Max impulse | Min robot | Max robot |
| 1 | 500 | 2500 | -PI/2 | PI/2 |
| 2 | 500 | 2500 | PI | 0 |
| 3 | 600 | 2600 | -PI/2 | PI/2 |
| 4 | 500 | 2500 | -PI/2 | PI/2 |
int jointToImp(double x,int i) { int imp=(x - joint_min[i]) * (imp_max[i]-imp_min[i]) / (joint_max[i]-joint_min[i]) + imp_min[i]; imp=max(imp,imp_min[i]); imp=min(imp,imp_max[i]); return imp; }
Envoyer une commande au servomoteur
Pour piloter les servomoteurs, nous utilisons la librairie Servo.h disponible de base dans l’IDE d’Arduino. Nous écrivons une fonction qui envoie la commande PWM à chaque servomoteur en fonction de l’angle demandé.
void servoToImp(double q[nbLinks],int velocity){ for (int i=0; i<nbLinks; i++) { servo[i].writeMicroseconds(jointToImp(q[i],i)); delay(velocity); } }
Fonction permettant le contrôle du robot
Pour contrôler les servomoteurs, il faut, à chaque instant, comparer la position désirée du robot à sa position actuelle
On calcul donc la position du robot en fonction des angles moteurs. Pour cela nous utilisons les matrices de transformation définies par la méthode de Denavit-Hartenberg.
forwardKinematics(sig,a,al,d,th,q,nbLinks,X);
On applique le contrôleur pour calculer la prochaine position du robot
circleTraj(20,165,0,20,k,Te,Xd); circleTraj(20,165,0,20,k+1,Te,Xk); for(int i=0;i<6;i++) Xu[i]=(Xk[i]-Xd[i]+gain*Te*(Xd[i]-X[i]));
On détermine les angles moteurs pour atteindre la prochaine position
for(int i=0;i<nbLinks;i++) qN1[i]=q[i]; computeAngle(); for(int i=0;i<nbLinks;i++) q[i]=qN1[i]+qu[i];
On applique la commande PWM à chaque servomoteur
servoToImp(q,10);
Code complet
Librairie personnalisée à partir de MatrixMath.h, MatrixMathExt.h
/*****************************************************************\ * Project : Handy * Author : X. Wiedmer * Version : V01 * Date : 08/06/2017 * Revision : * Summary : \*****************************************************************/ // Library #include <SoftwareSerial.h> #include <Servo.h> #include <MatrixMathExt.h> // Pin assignement #define BASE 2 #define SHOULDER 3 #define ARM 4 #define FOREARM 5 #define WRIST 6 //paramètres Denavit-Hartenberg const double baseLength = 45;//mm const double shoulderLength = 10;//mm const double armLength = 75;//mm const double forearmLength = 75;//mm const double wristLength = 40;//mm const int nbLinks=4; double sig[nbLinks]={0,0,0,0}; double a[nbLinks]={0,armLength,forearmLength,wristLength}; double al[nbLinks]={PI/2,0,0,0}; double d[nbLinks]={baseLength,0,0,0}; double th[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2}; double restPos[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2}; //paramètres servomoteur const int servoPin[nbLinks]={BASE,SHOULDER,ARM,FOREARM}; Servo servo[nbLinks]; const double joint_min[nbLinks]={-PI/2,PI,-2*PI/3,-PI/2}; const double joint_max[nbLinks]={PI/2,0,PI/2,PI/2}; const int imp_min[nbLinks]={500,500,600,500}; const int imp_max[nbLinks]={2500,2500,2600,2500}; //paramètre du contrôle double Te=0.01; // pas de temps du contrôleur double gain=30; // gain du contrôle int N=(int)2/Te+1; // nombre d'étape pour parcourir 2 fois le cercle // Variables float X[6],Xd[6],Xk[6],Xu[6]; double qN1[nbLinks],qu[nbLinks]; double q[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2}; int firstShot = 0; // Pour que le programme ne s'exécute qu'une fois /******************************************************************\ * PRIVATE FUNCTION: setup * * PARAMETERS: * ~ void * * RETURN: * ~ void * * DESCRIPTIONS: * Initiate inputs/outputs * \******************************************************************/ void setup(){ Serial.begin(9600); // Initialise le port série for (int i=0; i<nbLinks; i++) { // Initiatlise et positionne les servomoteurs au démarrage servo[i].writeMicroseconds(jointToImp(0,i)); servo[i].attach(servoPin[i]); delay(500); } } /******************************************************************\ * PRIVATE FUNCTION: loop * * PARAMETERS: * ~ void * * RETURN: * ~ void * * DESCRIPTIONS: * Main Function of the code \******************************************************************/ void loop(){ if (firstShot == 0){ //follow trajectory for(int k=0;k<N;k++){ //Calcule la position du robot forwardKinematics(sig,a,al,d,th,q,nbLinks,X); //Calcule la prochaine position circleTraj(20,165,0,20,k,Te,Xd); circleTraj(20,165,0,20,k+1,Te,Xk); for(int i=0;i<6;i++) Xu[i]=(Xk[i]-Xd[i]+gain*Te*(Xd[i]-X[i])); //Calcule les angles moteurs pour atteindre la prochaine position for(int i=0;i<nbLinks;i++) qN1[i]=q[i]; computeAngle(); for(int i=0;i<nbLinks;i++) q[i]=qN1[i]+qu[i]; //Envoie la commande au servomoteur servoToImp(q,10); // Affiche les angles moteur à chaque itération Serial.print("-----------------Iteration "); Serial.println(k); Serial.print("angle base = "); Serial.println(q[0]); Serial.print("angle bras = "); Serial.println(q[1]); Serial.print("angle avant-bras = "); Serial.println(q[2]); Serial.print("angle poignet = "); Serial.println(q[3]); } firstShot=1; } if(firstShot==1){ Serial.println("robot au repos"); restR(); Serial.println("robot stop"); stopR(); firstShot=2; } } // Decrit la trajectoire dans l'espace en focntion du temps void circleTraj(double R,double x,double y,double z,int i,double Te, float Xd[6]){ Xd[0]=x+R*cos(2*PI*Te*i); Xd[1]=y+R*sin(2*PI*Te*i); Xd[2]=z; Xd[3]=0; Xd[4]=0; Xd[5]=0; } // Calcule la matrice de transformation d'un lien robotique void computeLinkTransform(double a,double al,double d, double th, float T[][4]){ float trans[4][4] = {{cos(th), -sin(th)*cos(al), sin(th)*sin(al), a*cos(th)}, {sin(th), cos(th)*cos(al), -cos(th)*sin(al), a*sin(th)}, { 0, sin(al), cos(al), d }, { 0, 0, 0, 1 } }; Matrix.Copy((float*)trans,4,4,(float*)T); } // Calcule la position de la chaine robotique void forwardKinematics(double* sig,double* a,double* al,double* d,double* th,double* q, int nbLinks, float X[6]){ float A[4][4]={{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}; float R[4][4]; float Ti[4][4]; // Compute transformation matrix for (int i=0; i<nbLinks; i++){ if (sig[i]==0){ th[i]=q[i]; }else{ d[i]=q[i]; } //A=A*Ti computeLinkTransform(a[i],al[i],d[i],th[i],Ti); Matrix.Multiply((float*)A, (float*)Ti,4, 4,4, (float*)R); Matrix.Copy((float*)R,4,4,(float*)A); } X[0]=A[0][3]; X[1]=A[1][3]; X[2]=A[2][3]; X[3]=0; X[4]=0; X[5]=0; } // Calcule un produit vectoriel void CrossProduct1D(float* a, float* b, float* r){ /*Ex: double v1[3]={1,0,0}; double v2[3]={0,0,1}; double w[3]; CrossProduct1D(v1,v2,w);*/ r[0] = a[1]*b[2]-a[2]*b[1]; r[1] = a[2]*b[0]-a[0]*b[2]; r[2] = a[0]*b[1]-a[1]*b[0]; } // Calcule la matrice jacobienne d'une chaine robotique void jacobian(double* sig,double* a,double* al,double* d,double* th,double* q, int nbLinks, float* J){ float Ti[4][4]; float O[nbLinks+1][3]; float z[nbLinks+1][3]; float A[4][4]={{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}; float R[4][4]; float v[4]; O[0][0]=0; O[0][1]=0; O[0][2]=0; z[0][0]=0; z[0][1]=0; z[0][2]=1; float v0[4]={0,0,1,1}; for (int i=0; i<nbLinks; i++){ // Compute transformation matrix if (sig[i]==0){ th[i]=q[i]; }else{ d[i]=q[i]; } computeLinkTransform(a[i],al[i],d[i],th[i],Ti); // A=A*T[j]; Matrix.Multiply((float*)A, (float*)Ti,4, 4,4, (float*)R); Matrix.Copy((float*)R,4,4,(float*)A); //Compute joint center and orientation vector O[i+1][0]=A[0][3]; O[i+1][1]=A[1][3]; O[i+1][2]=A[2][3]; Matrix.Multiply((float*)A, (float*)v0,4, 4,1, (float*)v); //z{i}=[v(1); v(2); v(3)]-O{i}; z[i+1][0]=v[0]-O[i+1][0]; z[i+1][1]=v[1]-O[i+1][1]; z[i+1][2]=v[2]-O[i+1][2]; } //Jacobian float tempv[3]; float cprod[3]; for(int i=0;i<nbLinks;i++){ if (sig[i]==0){ // Ji=[z(i-1)xON-O(i-1); z(i-1)] Matrix.Subtract((float*)O[nbLinks], (float*)O[i],1,3,(float*)tempv); CrossProduct1D(z[i],tempv,cprod); J[0*nbLinks+i]=cprod[0]; J[1*nbLinks+i]=cprod[1]; J[2*nbLinks+i]=cprod[2]; J[3*nbLinks+i]=z[i][0]; J[4*nbLinks+i]=z[i][1]; J[5*nbLinks+i]=z[i][2]; }else{ J[0*nbLinks+i]=z[i][0]; J[1*nbLinks+i]=z[i][1]; J[2*nbLinks+i]=z[i][2]; J[3*nbLinks+i]=0; J[4*nbLinks+i]=0; J[5*nbLinks+i]=0; } } } // Calcul le déterminant d'une matrice float detrm(float a[nbLinks][nbLinks],float k) { float s=1,det=0,b[nbLinks][nbLinks]; int i,j,m,n,c; if(k==1) { return(a[0][0]); } else { det=0; for(c=0;c<k;c++) { m=0; n=0; for(i=0;i<k;i++) { for(j=0;j<k;j++) { b[i][j]=0; if(i!=0&&j!=c) { b[m][n]=a[i][j]; if(n<(k-2)) n++; else { n=0; m++; } } } } det=det+s*(a[0][c]*detrm(b,k-1)); s=-1*s; } } return(det); } // Calcule les angles moteur en fonction de la position désirée void computeAngle(){ float J[6][nbLinks]; float Jt[nbLinks][6]; float JJt[nbLinks][nbLinks]; float invJ[nbLinks][6]; double detJ; // compute jacobian jacobian(sig,a,al,d,th,q,nbLinks,(float*)J); // avoid singularity Matrix.Transpose((float*)J,6,nbLinks,(float*)Jt); Matrix.Multiply((float*)Jt, (float*)J, nbLinks, 6, nbLinks,(float*)JJt); detJ=detrm(JJt,nbLinks); // invert jacobian if(detJ>=1){ Matrix.Invert((float*)JJt,nbLinks); Matrix.Multiply((float*)JJt,(float*)Jt,nbLinks,nbLinks,6,(float*)invJ); } for(int i=0;i<nbLinks;i++){ qu[i]=0; for(int j=0;j<6;j++){ qu[i]+=invJ[i][j]*Xu[j]; } } } // Convertie l'angle moteur en commande PWM int jointToImp(double x,int i) { int imp=(x - joint_min[i]) * (imp_max[i]-imp_min[i]) / (joint_max[i]-joint_min[i]) + imp_min[i]; imp=max(imp,imp_min[i]); imp=min(imp,imp_max[i]); return imp; } // Intitialise servomoteur void servoAttach(){ for (int i=0; i<nbLinks; i++) { servo[i].attach(servoPin[i]); } } // Envoie la commande PWM à chaque servomoteur void servoToImp(double q[nbLinks],int velocity){ for (int i=0; i<nbLinks; i++) { servo[i].writeMicroseconds(jointToImp(q[i],i)); delay(velocity); } } // Met le robot en position de repos void restR(){ servoToImp(restPos,500); } // Déconnecte les servomoteurs void stopR(){ for(int j=0;j<nbLinks;j++){ servo[j].detach(); } }
Résultat
Le moteur dessine sur la feuille et suit la trajectoire définie.
Si vous souhaitez de l’aide avec votre bras robotisé ou si vous désirez plus d’information sur ce projet, n’hésitez pas à laisser un commentaire ou à nous contacter.
Référence
Vous pouvez retrouver le robot ici.


Bon travail! Bon courage pour la suite
bon travail
Merci beaucoup!