A good exercise for programmation is to make a robotic arm reproduce a trajectory, such as drawing on a piece of paper. Once you have this knowledge, a robotic arm can be programmed to do anything you want.
Material
- Robotic arm Handy
- 4x Servomotor SMS1012
- Servodriver
- 5V power supply
- USB cable
- Arduino UNO
Objectif
Obj: Make a robot draw
To realize this project, we need to:
- Mount the robotic arm (Structure)
- Link the electronics to the motor and power to allow the control of the arm (Hardware)
- Write the program to make the robot follow a trajectory (Software)
Structure
Obj: The structure should be able to carry a pen in three dimensions of space.
We used a desktop robotic arm Handy for this project. The parts are optimized for a tiny servomotor and were printed from base to wrist. An aditional pen holder was designed and printed.
that you can download here. The arm is mounted with 4 micro servomotors and the base is attached to a wooden plate.

Hardware
Obj: The board should be linked to servomotor and power supply in order to control the servomotor with a PWM signal.
- arduino UNO
Arduino board was picked, they are easy to use and there is huge community to ask for help. As the program ask for a bit of memory we chose a Arduino UNO.
- Servo driver
The arduino cannot power so much servomotors. A driver need to be add to distribute the power from another source.
This tutorial was followed to make the driver.

Software
Objectives
;
The objective of the program can be divided in smaller tasks:
- Describe the trajectory coordinates in space
- Transform the coordintates of the trajectory into the desired angles of the robot joints.
- Control the robot position
- Convert robot angles into servomotor command value
- Send command to servomotor
Describe the trajectory coordinates in space
The trajectory chosen is a circle for its simplicity. The parametric equations are :
For the z coordinates, we take the pen height with respect to the wrist: 20mm.
We write a function that output the desired position with respect to the time step:
void circleTraj(double R,double x,double y,double z,int i,double Te, float Xd[6]){ Xd[0]=x+R*cos(2*PI*Te*i); Xd[1]=y+R*sin(2*PI*Te*i); Xd[2]=z; Xd[3]=0; Xd[4]=0; Xd[5]=0; }
Transform the coordintates of the trajectory into the desired angles of the robot joints
The robotic arm can be described with the Denavit-Hartenberg mehtod as a robotic chain with 4 articulated links. This method is interesting to controle articulated projects with more than 3 articulations.
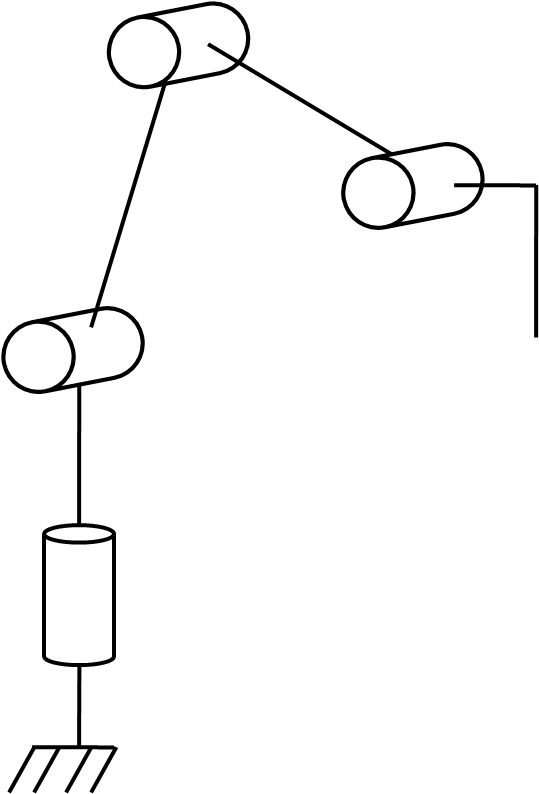
The method defines a cartesian frame for each joint following the same logic which result in the definition of parameters that can be used to describe mathematically the movement of the links.
Definition of the parameters with respect to geometry (DH parameters)
| j | Sigmaj | Thetaj | Dj (mm) | Aj (mm) | alphaj |
| 1 | 0 | Th1 | 45 | 0 | 90 |
| 2 | 0 | Th2 | 0 | 75 | 0 |
| 3 | 0 | Th3 | 0 | 75 | 0 |
| 4 | 0 | Th4 | 4 | 0 | -90 |
To compute the desired angles from the desired position we use the inverse of the jacobian matrix defined with the denavit-hartenberg parameters. To compute matrices we use MatrixMath.h library
void computeAngle(){ float J[6][nbLinks]; float Jt[nbLinks][6]; float JJt[nbLinks][nbLinks]; float invJ[nbLinks][6]; double detJ; // compute jacobian jacobian(sig,a,al,d,th,q,nbLinks,(float*)J); // avoid singularity Matrix.Transpose((float*)J,6,nbLinks,(float*)Jt); Matrix.Multiply((float*)Jt, (float*)J, nbLinks, 6, nbLinks,(float*)JJt); detJ=detrm(JJt,nbLinks); // invert jacobian if(detJ>=1){ Matrix.Invert((float*)JJt,nbLinks); Matrix.Multiply((float*)JJt,(float*)Jt,nbLinks,nbLinks,6,(float*)invJ); } for(int i=0;i<nbLinks;i++){ qu[i]=0; for(int j=0;j<6;j++){ qu[i]+=invJ[i][j]*Xu[j]; } } }
Convert joint angle into servomotor command
In order to convert angles to PWM command, servomotor position with respect to the joint and PWM nominal values should be known. This conversion also depends on the cartesian frames used to describe the mechanical link with DH method.
| Servo/Joint | Min impulse | Max impulse | Min robot | Max robot |
| 1 | 500 | 2500 | -PI/2 | PI/2 |
| 2 | 500 | 2500 | PI | 0 |
| 3 | 600 | 2600 | -PI/2 | PI/2 |
| 4 | 500 | 2500 | -PI/2 | PI/2 |
int jointToImp(double x,int i) { int imp=(x - joint_min[i]) * (imp_max[i]-imp_min[i]) / (joint_max[i]-joint_min[i]) + imp_min[i]; imp=max(imp,imp_min[i]); imp=min(imp,imp_max[i]); return imp; }
Send command to servomotor
To drive the servomotors, we use the basic Servo.h library available in the Arduino IDE. We write a function that sends the PWM command to each servomotor according to the requested angle.
void servoToImp(double q[nbLinks],int velocity){ for (int i=0; i<nbLinks; i++) { servo[i].writeMicroseconds(jointToImp(q[i],i)); delay(velocity); } }
Control the robot position
To control servomotors, desired and actual position must be compared in real time
Robot position is compute with the angle of the joints using the transformtaion matrices defined with the denavit-hartenberg method.
forwardKinematics(sig,a,al,d,th,q,nbLinks,X);
Controle is applied to compute the next desired position
circleTraj(20,165,0,20,k,Te,Xd); circleTraj(20,165,0,20,k+1,Te,Xk); for(int i=0;i<6;i++) Xu[i]=(Xk[i]-Xd[i]+gain*Te*(Xd[i]-X[i]));
The desired servomotor angles are computed to reache the next desired position
for(int i=0;i<nbLinks;i++) qN1[i]=q[i]; computeAngle(); for(int i=0;i<nbLinks;i++) q[i]=qN1[i]+qu[i];
PWM command is apply for every servo.
servoToImp(q,10);
Complete code
Customized library based on MatrixMath.h , MatrixMathExt.h
/*****************************************************************\ * Project : Handy * Author : X. Wiedmer * Version : V01 * Date : 08/06/2017 * Revision : * Summary : \*****************************************************************/ // Library #include <SoftwareSerial.h> #include <Servo.h> #include <MatrixMathExt.h> // Pin assignement #define BASE 2 #define SHOULDER 3 #define ARM 4 #define FOREARM 5 #define WRIST 6 //paramètres Denavit-Hartenberg const double baseLength = 45;//mm const double shoulderLength = 10;//mm const double armLength = 75;//mm const double forearmLength = 75;//mm const double wristLength = 40;//mm const int nbLinks=4; double sig[nbLinks]={0,0,0,0}; double a[nbLinks]={0,armLength,forearmLength,wristLength}; double al[nbLinks]={PI/2,0,0,0}; double d[nbLinks]={baseLength,0,0,0}; double th[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2}; double restPos[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2}; //paramètres servomoteur const int servoPin[nbLinks]={BASE,SHOULDER,ARM,FOREARM}; Servo servo[nbLinks]; const double joint_min[nbLinks]={-PI/2,PI,-2*PI/3,-PI/2}; const double joint_max[nbLinks]={PI/2,0,PI/2,PI/2}; const int imp_min[nbLinks]={500,500,600,500}; const int imp_max[nbLinks]={2500,2500,2600,2500}; //paramètre du contrôle double Te=0.01; // pas de temps du contrôleur double gain=30; // gain du contrôle int N=(int)2/Te+1; // nombre d'étape pour parcourir 2 fois le cercle // Variables float X[6],Xd[6],Xk[6],Xu[6]; double qN1[nbLinks],qu[nbLinks]; double q[nbLinks]={0,3*PI/4,-PI/2,-3*PI/4+PI/2}; int firstShot = 0; // Pour que le programme ne s'exécute qu'une fois /******************************************************************\ * PRIVATE FUNCTION: setup * * PARAMETERS: * ~ void * * RETURN: * ~ void * * DESCRIPTIONS: * Initiate inputs/outputs * \******************************************************************/ void setup(){ Serial.begin(9600); // Initialise le port série for (int i=0; i<nbLinks; i++) { // Initiatlise et positionne les servomoteurs au démarrage servo[i].writeMicroseconds(jointToImp(0,i)); servo[i].attach(servoPin[i]); delay(500); } } /******************************************************************\ * PRIVATE FUNCTION: loop * * PARAMETERS: * ~ void * * RETURN: * ~ void * * DESCRIPTIONS: * Main Function of the code \******************************************************************/ void loop(){ if (firstShot == 0){ //follow trajectory for(int k=0;k<N;k++){ //Calcule la position du robot forwardKinematics(sig,a,al,d,th,q,nbLinks,X); //Calcule la prochaine position circleTraj(20,165,0,20,k,Te,Xd); circleTraj(20,165,0,20,k+1,Te,Xk); for(int i=0;i<6;i++) Xu[i]=(Xk[i]-Xd[i]+gain*Te*(Xd[i]-X[i])); //Calcule les angles moteurs pour atteindre la prochaine position for(int i=0;i<nbLinks;i++) qN1[i]=q[i]; computeAngle(); for(int i=0;i<nbLinks;i++) q[i]=qN1[i]+qu[i]; //Envoie la commande au servomoteur servoToImp(q,10); // Affiche les angles moteur à chaque itération Serial.print("-----------------Iteration "); Serial.println(k); Serial.print("angle base = "); Serial.println(q[0]); Serial.print("angle bras = "); Serial.println(q[1]); Serial.print("angle avant-bras = "); Serial.println(q[2]); Serial.print("angle poignet = "); Serial.println(q[3]); } firstShot=1; } if(firstShot==1){ Serial.println("robot au repos"); restR(); Serial.println("robot stop"); stopR(); firstShot=2; } } // Decrit la trajectoire dans l'espace en focntion du temps void circleTraj(double R,double x,double y,double z,int i,double Te, float Xd[6]){ Xd[0]=x+R*cos(2*PI*Te*i); Xd[1]=y+R*sin(2*PI*Te*i); Xd[2]=z; Xd[3]=0; Xd[4]=0; Xd[5]=0; } // Calcule la matrice de transformation d'un lien robotique void computeLinkTransform(double a,double al,double d, double th, float T[][4]){ float trans[4][4] = {{cos(th), -sin(th)*cos(al), sin(th)*sin(al), a*cos(th)}, {sin(th), cos(th)*cos(al), -cos(th)*sin(al), a*sin(th)}, { 0, sin(al), cos(al), d }, { 0, 0, 0, 1 } }; Matrix.Copy((float*)trans,4,4,(float*)T); } // Calcule la position de la chaine robotique void forwardKinematics(double* sig,double* a,double* al,double* d,double* th,double* q, int nbLinks, float X[6]){ float A[4][4]={{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}; float R[4][4]; float Ti[4][4]; // Compute transformation matrix for (int i=0; i<nbLinks; i++){ if (sig[i]==0){ th[i]=q[i]; }else{ d[i]=q[i]; } //A=A*Ti computeLinkTransform(a[i],al[i],d[i],th[i],Ti); Matrix.Multiply((float*)A, (float*)Ti,4, 4,4, (float*)R); Matrix.Copy((float*)R,4,4,(float*)A); } X[0]=A[0][3]; X[1]=A[1][3]; X[2]=A[2][3]; X[3]=0; X[4]=0; X[5]=0; } // Calcule un produit vectoriel void CrossProduct1D(float* a, float* b, float* r){ /*Ex: double v1[3]={1,0,0}; double v2[3]={0,0,1}; double w[3]; CrossProduct1D(v1,v2,w);*/ r[0] = a[1]*b[2]-a[2]*b[1]; r[1] = a[2]*b[0]-a[0]*b[2]; r[2] = a[0]*b[1]-a[1]*b[0]; } // Calcule la matrice jacobienne d'une chaine robotique void jacobian(double* sig,double* a,double* al,double* d,double* th,double* q, int nbLinks, float* J){ float Ti[4][4]; float O[nbLinks+1][3]; float z[nbLinks+1][3]; float A[4][4]={{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}; float R[4][4]; float v[4]; O[0][0]=0; O[0][1]=0; O[0][2]=0; z[0][0]=0; z[0][1]=0; z[0][2]=1; float v0[4]={0,0,1,1}; for (int i=0; i<nbLinks; i++){ // Compute transformation matrix if (sig[i]==0){ th[i]=q[i]; }else{ d[i]=q[i]; } computeLinkTransform(a[i],al[i],d[i],th[i],Ti); // A=A*T[j]; Matrix.Multiply((float*)A, (float*)Ti,4, 4,4, (float*)R); Matrix.Copy((float*)R,4,4,(float*)A); //Compute joint center and orientation vector O[i+1][0]=A[0][3]; O[i+1][1]=A[1][3]; O[i+1][2]=A[2][3]; Matrix.Multiply((float*)A, (float*)v0,4, 4,1, (float*)v); //z{i}=[v(1); v(2); v(3)]-O{i}; z[i+1][0]=v[0]-O[i+1][0]; z[i+1][1]=v[1]-O[i+1][1]; z[i+1][2]=v[2]-O[i+1][2]; } //Jacobian float tempv[3]; float cprod[3]; for(int i=0;i<nbLinks;i++){ if (sig[i]==0){ // Ji=[z(i-1)xON-O(i-1); z(i-1)] Matrix.Subtract((float*)O[nbLinks], (float*)O[i],1,3,(float*)tempv); CrossProduct1D(z[i],tempv,cprod); J[0*nbLinks+i]=cprod[0]; J[1*nbLinks+i]=cprod[1]; J[2*nbLinks+i]=cprod[2]; J[3*nbLinks+i]=z[i][0]; J[4*nbLinks+i]=z[i][1]; J[5*nbLinks+i]=z[i][2]; }else{ J[0*nbLinks+i]=z[i][0]; J[1*nbLinks+i]=z[i][1]; J[2*nbLinks+i]=z[i][2]; J[3*nbLinks+i]=0; J[4*nbLinks+i]=0; J[5*nbLinks+i]=0; } } } // Calcul le déterminant d'une matrice float detrm(float a[nbLinks][nbLinks],float k) { float s=1,det=0,b[nbLinks][nbLinks]; int i,j,m,n,c; if(k==1) { return(a[0][0]); } else { det=0; for(c=0;c<k;c++) { m=0; n=0; for(i=0;i<k;i++) { for(j=0;j<k;j++) { b[i][j]=0; if(i!=0&&j!=c) { b[m][n]=a[i][j]; if(n<(k-2)) n++; else { n=0; m++; } } } } det=det+s*(a[0][c]*detrm(b,k-1)); s=-1*s; } } return(det); } // Calcule les angles moteur en fonction de la position désirée void computeAngle(){ float J[6][nbLinks]; float Jt[nbLinks][6]; float JJt[nbLinks][nbLinks]; float invJ[nbLinks][6]; double detJ; // compute jacobian jacobian(sig,a,al,d,th,q,nbLinks,(float*)J); // avoid singularity Matrix.Transpose((float*)J,6,nbLinks,(float*)Jt); Matrix.Multiply((float*)Jt, (float*)J, nbLinks, 6, nbLinks,(float*)JJt); detJ=detrm(JJt,nbLinks); // invert jacobian if(detJ>=1){ Matrix.Invert((float*)JJt,nbLinks); Matrix.Multiply((float*)JJt,(float*)Jt,nbLinks,nbLinks,6,(float*)invJ); } for(int i=0;i<nbLinks;i++){ qu[i]=0; for(int j=0;j<6;j++){ qu[i]+=invJ[i][j]*Xu[j]; } } } // Convertie l'angle moteur en commande PWM int jointToImp(double x,int i) { int imp=(x - joint_min[i]) * (imp_max[i]-imp_min[i]) / (joint_max[i]-joint_min[i]) + imp_min[i]; imp=max(imp,imp_min[i]); imp=min(imp,imp_max[i]); return imp; } // Intitialise servomoteur void servoAttach(){ for (int i=0; i<nbLinks; i++) { servo[i].attach(servoPin[i]); } } // Envoie la commande PWM à chaque servomoteur void servoToImp(double q[nbLinks],int velocity){ for (int i=0; i<nbLinks; i++) { servo[i].writeMicroseconds(jointToImp(q[i],i)); delay(velocity); } } // Met le robot en position de repos void restR(){ servoToImp(restPos,500); } // Déconnecte les servomoteurs void stopR(){ for(int j=0;j<nbLinks;j++){ servo[j].detach(); } }
Result
The robot follow the trajectory and is able to draw a circle on the paper
If you want more information on this project don’t hesitate to leave a comment or to send us a message.
Sources
You can purchase this robot here.




